Variational Autoencoder

Variational Autoencoders (VAEs) are a class of generative models that are widely used in machine learning for their ability to learn efficient latent representations of data. They extend traditional/vanilla autoencoders by imposing a probabilistic structure on the latent space, making them capable of generating new data samples.

The key idea behind VAEs is to map high-dimensional input data to a lower-dimensional latent space, from which new data points can be sampled and decoded back to the original input space.

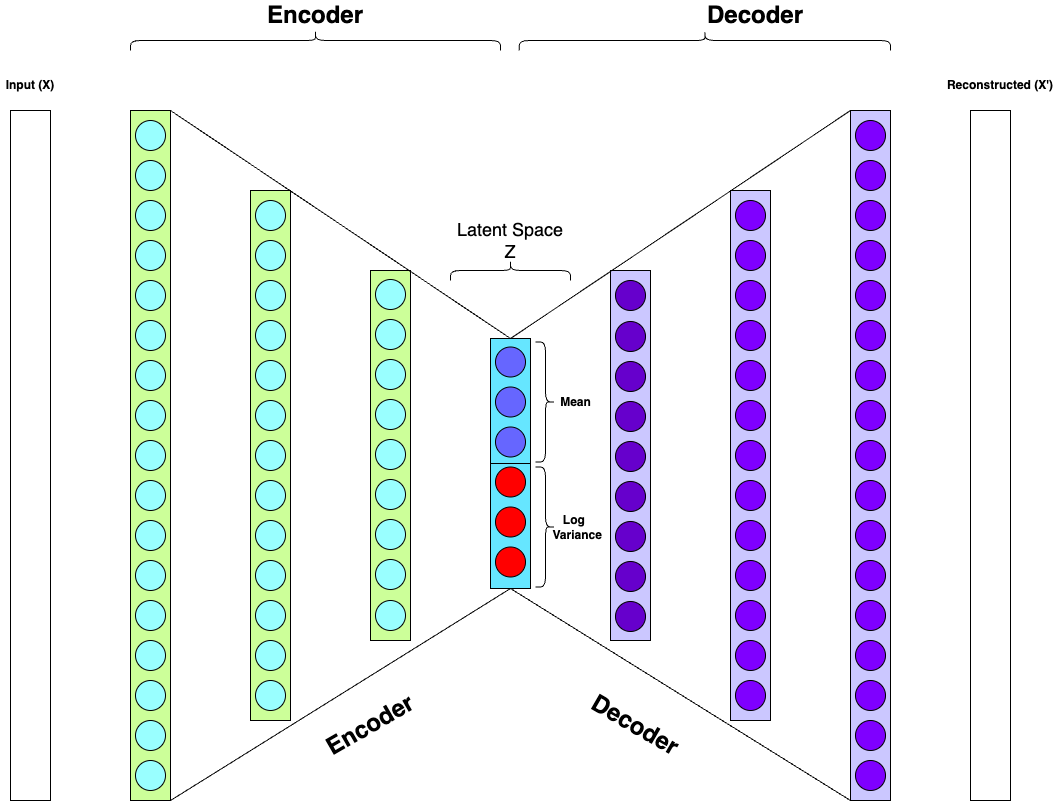
Figure (i) by KB designed using draw.io

The VAE Architecture

A VAE consists of two main components: the encoder and the decoder.

Encoder: Maps the input data to a latent space by outputting two vectors: the mean (μ) and the log-variance (log(σ²)) of the latent distribution.
Decoder: Uses a sampled latent vector to reconstruct the original data from the lower-dimensional latent space.

These two components are trained simultaneously to minimize the reconstruction error and the Kullback-Leibler (KL) divergence between the learned latent distribution and a prior distribution (typically a standard Gaussian).

The goal of a VAE is to learn a distribution \(p(x)\) that best approximates the data \(x\) by sampling latent variables \(z\) from a learned distribution \(q(z|x)\) and using these to reconstruct the data \(x\).

Reparameterization Trick

In Variational Autoencoders (VAEs), the encoder network maps an input \(x\) to a distribution over the latent space. This distribution is typically Gaussian with a mean \(\mu\) and a variance \(\sigma^2\). To generate the latent variable \(z\), we would ideally sample it from this distribution. The problem arises, however, with the sampling process itself. Sampling introduces stochasticity (randomness), which disrupts the backpropagation process needed for training the model.

The core challenge is that backpropagation requires a differentiable function, i.e a full deterministic computational graph. However, the operation of drawing a random sample from the Gaussian distribution is not deterministic. This is a significant issue for training the encoder network, as backpropagation would fail without a method to handle this stochastic step.

The reparameterization trick is a technique that addresses this problem by re-expressing the sampling process in a way that allows gradients to propagate through it. Instead of directly sampling \(z\) from the Gaussian distribution, we reparameterize the latent variable \(z\) as a deterministic function of \(\mu\), \(\sigma\), and a random noise term \(\epsilon\) drawn from a standard normal distribution \( \mathcal{N}(0, 1)\). Specifically, the reparameterization is expressed as:

\( z = \mu + \sigma \cdot \epsilon \), where \(\epsilon \sim \mathcal{N}(0, 1)\)

Here, \(\mu\) and \(\sigma\) are the mean and standard deviation of the latent distribution, which are both outputs of the encoder network. The term \(\epsilon\) represents random noise drawn from a standard normal distribution, which introduces the randomness into the latent variable. This formulation has a key advantage: \(z\) is now expressed as a deterministic function of \(\mu\), \(\sigma\), and \(\epsilon\), where the randomness is isolated in \(\epsilon\), which does not depend on the network parameters. This means that the values of \(\mu\) and \(\sigma\) are directly controlled by the network, and gradients can be backpropagated through them during training.

Intuition

To understand this intuitively, consider that \(\mu\) and \(\sigma\) control the location (mean) and spread (variance) of the latent distribution. I will show what this means with an actual coding implementation as well as a visualization of the latent space in 3D. Think of the reparameterization trick as "shifting and scaling" the randomness (\(\epsilon\)):

\(\mu\) shifts the distribution.
\(\sigma\) scales the distribution.

The reparameterization trick allows the model to preserve the stochasticity of the latent variable while ensuring that the process remains differentiable and trainable via backpropagation.

ELBO (Evidence Lower Bound):

A Variational Autoencoder (VAE) learns a probabilistic mapping from a high-dimensional data space \( x \) to a lower-dimensional latent space \( z \). The objective of the VAE is to maximize the likelihood of the data, but instead of directly maximizing \( p(x) \), we maximize the Evidence Lower Bound (ELBO) due to the intractability of the marginal likelihood.

The VAE maximizes the ELBO, which is a lower bound on the log-likelihood of the data:

\( \log p(x) \geq \mathbb{E}_{q(z|x)}[\log p(x|z)] - \text{KL}(q(z|x) \parallel p(z)) \)

Where:

\( p(x) \) is the marginal likelihood (the probability of the data).
\( q(z|x) \) is the approximate posterior distribution of the latent variable \( z \) given the input \( x \).
\( p(x|z) \) is the likelihood of the data given the latent variable \( z \) (the decoder network).
\( p(z) \) is the prior distribution over the latent variable \( z \), often chosen as a standard normal \( \mathcal{N}(0, I) \).
The second term is the **KL divergence** which penalizes the divergence between the learned posterior and the prior.

KL Divergence:

The KL divergence between the approximate posterior \( q(z|x) \) and the prior \( p(z) \) is computed as:

\( \text{KL}(q(z|x) \parallel p(z)) = -\frac{1}{2} \left( 1 + \log(\sigma^2) - \mu^2 - \sigma^2 \right) \)

Where:

\( \mu \) and \( \sigma^2 \) are the mean and variance of the approximate posterior distribution \( q(z|x) = \mathcal{N}(\mu(x), \sigma^2(x)) \).
\( p(z) = \mathcal{N}(0, I) \) is the standard normal prior over \( z \).

VAE Loss Function:

The total loss function for the VAE combines the reconstruction loss and the KL divergence term:

\( \mathcal{L} = -\mathbb{E}_{q(z|x)}[\log p(x|z)] + \text{KL}(q(z|x) \parallel p(z)) \)

The reconstruction loss ensures that the decoder can generate accurate data samples from the latent variable, while the KL divergence ensures that the learned latent distribution is close to the prior, helping with regularization.

An Implementation

An implementation of a variational autoencoder is here: https://github.com/KrishnaMBhattarai/VariationalAutoencoder

You can also open the notebook with Google Colab directly: https://colab.research.google.com/github/KrishnaMBhattarai/VariationalAutoencoder/blob/main/VariationalAutoencoder.ipynb

Let's look at it here as well:

import torch
import torch.nn as nn
import torch.nn.functional as nn_functional
import torch.optim as optim
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
import numpy as np
import plotly.express as px

# Let's define the model architecture
class VariationalAutoencoder(nn.Module):
    def __init__(self, input_dim=784, hidden_dim=392, latent_dim=3):
        super(VariationalAutoencoder, self).__init__()               # initialize the VariationalAutoencoder class

        # lets define the encoder architecture as a sequential container
        self.encoder = nn.Sequential(
            nn.Linear(input_dim, hidden_dim),     # first Linear layer: input_dim -> hidden_dim.
            nn.LeakyReLU(0.3),                    # apply LeakyReLU with a negative solve of 0.3
            nn.Linear(hidden_dim, hidden_dim),    # second Linear layer: hidden_dim -> hidden_dim
            nn.LeakyReLU(0.3)                     # apply LeakyReLU activation
        )

        # lets define the Latent space layers
        self.mean_layer         = nn.Linear(hidden_dim, latent_dim)     # Linear layer to predict the mean (μ) of the latent gaussian distribution
        self.log_variance_layer = nn.Linear(hidden_dim, latent_dim)     # Linear layer to predict the log variance (log(σ²)) of the latent Gaussian distribution

        # lets define the decoder architecture as a sequential container
        self.decoder = nn.Sequential(
            nn.Linear(latent_dim, hidden_dim),    # a Linear layer: latent_dim -> hidden_dim
            nn.LeakyReLU(0.3),                    # apply LeakyReLU activation function with a negative solve of 0.3
            nn.Linear(hidden_dim, hidden_dim),    # another Linear layer: hidden_dim -> hidden_dim
            nn.LeakyReLU(0.3),                    # apply LeakyReLU activation function with a negative solve of 0.3
            nn.Linear(hidden_dim, input_dim),     # Final Linear layer: hidden_dim -> input_dim to reconstruct the input
            nn.Sigmoid()                          # Sigmoid activation function so that output values are squashed between 0 and 1
        )

def loss_function(reconstructed_x, x, latent_mean, latent_log_variance):

    # Reconstruction loss (binary cross-entropy)
    binary_cross_entropy = nn_functional.binary_cross_entropy(reconstructed_x, x.view(-1, 784), reduction='sum')

    # KL Divergence loss
    kl_divergence = -0.5 * torch.sum(1 + latent_log_variance - latent_mean.pow(2) - latent_log_variance.exp())

    return binary_cross_entropy + kl_divergence


def train(model, train_loader, optimizer, epoch):
    model.train()
    epoch_loss = 0

    for inputs, _ in train_loader:
        optimizer.zero_grad()

        # Forward pass
        reconstructed_inputs, latent_mean, latent_log_variance = model(inputs)

        # Compute loss
        batch_loss = loss_function(reconstructed_inputs, inputs, latent_mean, latent_log_variance)

        # Backward pass
        batch_loss.backward()

        epoch_loss += batch_loss.item()

        optimizer.step()

    print(f'Epoch: {epoch}, Average Loss: {epoch_loss / len(train_loader.dataset):.4f}')


def save_model(model, path='variational_autoencoder.pt'):
    torch.save(model.state_dict(), path)
    print(f"Model saved to {path}")


def load_model(model, path='variational_autoencoder.pt'):
    model.load_state_dict(torch.load(path))
    model.eval()                            # Set to evaluation mode
    print(f"Model loaded from {path}")
    return model

# # Check dataset size
print("Dataset size:", len(_train_dataset))

# Check the shape of one image and label
sample_image, sample_label = _train_dataset[0]
print("Image shape (C, H, W):", sample_image.shape)  # Should print torch.Size([1, 28, 28])
print("Label:", sample_label)

# Check batch shape
for images, labels in _train_loader:
    print("Batch image shape:", images.shape)   # [batch_size, 1, 28, 28]
    print("Batch labels shape:", labels.shape)  # [batch_size]
    break

# Display the first image to ensure it loads correctly
plt.imshow(sample_image[0], cmap='gray')  # [0] to remove the channel dimension for grayscale image
plt.title(f'Label: {sample_label}')
plt.axis('off')
plt.show()

# lets intialize the model and setup some hyperparameters for training
_model = VariationalAutoencoder()
_learning_rate = 1e-3

_optimizer = optim.Adam(_model.parameters(), lr=_learning_rate)

_epochs = 10

# # Training loop
for _epoch in range(1, _epochs + 1):
    train(_model, _train_loader, _optimizer, _epoch)

# lets save the model
save_model(_model)

# let us create an interactive 3d visualiztion of our latent space
import plotly.graph_objects as go

def visualize_latent_space(_model, _train_loader):
    _model.eval()  # Set the model to evaluation mode
    all_latent_vectors = []
    all_labels = []

    with torch.no_grad():
        for data, labels in _train_loader:  # Iterate through the DataLoader
            data = data.to(next(_model.parameters()).device)  # Move data to the same device as the model
            latent_mean, _, _ = _model.encode(data)  # Get the latent mean (μ) from the encoder
            all_latent_vectors.append(latent_mean.cpu())  # Move to CPU and store
            all_labels.append(labels.cpu())  # Store labels

    # Stack all latent vectors and labels into NumPy arrays
    latent_vectors = torch.cat(all_latent_vectors).numpy()
    labels = torch.cat(all_labels).numpy()

    # Create an interactive 3D scatter plot using Plotly
    fig = go.Figure()

    # Add a scatter plot for each unique label
    unique_labels = set(labels)
    for label in unique_labels:
        indices = labels == label
        fig.add_trace(go.Scatter3d(
            x=latent_vectors[indices, 0],
            y=latent_vectors[indices, 1],
            z=latent_vectors[indices, 2],
            mode='markers',
            marker=dict(size=5, opacity=0.7),
            name=f"Class|Digit {label}"
        ))

    # Customize layout
    fig.update_layout(
        title="Interactive 3D Latent Space Visualization",
        scene=dict(
            xaxis_title="Latent Dimension 1",
            yaxis_title="Latent Dimension 2",
            zaxis_title="Latent Dimension 3"
        ),
        height=800

    )

    # Save the figure to HTML

    fig.write_html("latent3d.html", full_html=True)
    fig.show()

# call the function above
visualize_latent_space(_model, _train_loader)

You can interact with this 3D visualization, you can rotate it and click on the labels on the right to turn some of them off as well. We can see that this visualization is a gold mine of information. It shows us where our model has things grouped together in 3D space, and where which ones overlap.

# lets try to generate some images using the test data set

def reconstruct_images_from_test_dataset(model, test_loader, device):
    model.eval().to(device)
    original_images, reconstructed_images = [], []

    with torch.no_grad():
        for images, _ in test_loader:
            if len(original_images) >= 10: break  # Stop after 10 original and reconstructed image pairs

            images = images.to(device)
            reconstructed, _, _ = model(images)

            original_images.append(images[0].cpu())
            reconstructed_images.append(reconstructed[0].cpu())

    # Plot the original and reconstructed images
    fig, axes = plt.subplots(2, 10, figsize=(15, 4))
    for i in range(10):
        # Plot original images (top row)
        axes[0, i].imshow(original_images[i].view(28, 28).detach().numpy(), cmap='gray')
        axes[0, i].axis('off')
        axes[0, i].set_title(f'Original {i+1}', fontsize=7)

        # Plot reconstructed images (bottom row)
        axes[1, i].imshow(reconstructed_images[i].view(28, 28).detach().numpy(), cmap='gray')
        axes[1, i].axis('off')
        axes[1, i].set_title(f'Reconstruction {i+1}', fontsize=7)

    plt.subplots_adjust(wspace=0.3, hspace=0.5)  # Increase space between images
    plt.show()

# call the function above
reconstruct_images_from_test_dataset(_model, _test_loader, _device)

# now let us create a function that will sample from our latent space and generate new images based on random latent vectors
def generate_image_from_latent_space(model, device, n_samples=10):
    model.eval().to(device)  # Set the model to evaluation mode and move to device

    # Generate random latent vectors with shape (n_samples, latent_dim)
    latent_vectors = torch.randn(n_samples, 3).to(device)  # Latent space with 3 dimensions

    # Pass the latent vectors through the decoder to generate images
    with torch.no_grad():
        generated_images = model.decode(latent_vectors)

    # Plot the generated images
    fig, axes = plt.subplots(1, n_samples, figsize=(15, 4))
    for i, ax in enumerate(axes):
        ax.imshow(generated_images[i].view(28, 28).cpu().detach().numpy(), cmap='gray')
        ax.axis('off')
        ax.set_title(f'Sample {i+1}', fontsize=7)

    plt.show()

# call the function above
generate_image_from_latent_space(_model, _device, 10)

Use the interactive sliders below to generate samples from the latent 3d vector of your choosing in real time

VAE Image Generator

X: 0

Y: 0

Z: 0

Generated Image: